Chemical Kinetics NEET Previous Year Question Paper: NEET PYQ (Past 10 Year)

Chemical Kinetics NEET PYQ Analysis (2020-2025)

Chemical Kinetics helps aspirants learn about the Arrhenius equation and the collision theory of reactions. NEET chemistry chapter-wise weightage shows Chemical Kinetics holds 5% weightage. It is an important unit of the NEET chemistry syllabus. Attempting NEET PYQ chemical kinetics helps students identify important topics. The table below shows the number of questions that appeared in the previous years.

Chemical Kinetics NEET PYQ

Numerical-based questions from Chemical Kinetics appear in the NEET exam. To solve them in less time, an effective NEET preparation timetable is important. The timetable should include 2-3 hours daily for solving the NEET question paper. Provided below are a few NEET chemical kinetics previous year questions with solutions. Going through them makes students familiar with the question pattern.

Question 1: If the half-life $\left(\mathrm{t}_{1 / 2}\right)$ for a first-order reaction is 1 minute, then the time required for $99.9 \%$ completion of the reaction is closest to: (NEET 2025)

Options

1. 10 minutes

2. 2 minutes

3. 4 minutes

4. 5 minutes

Answer: For a first-order reaction-
$t=\frac{6.9}{k}$ for $\sim 99.9 \%$ completion (more accurately, $t=\frac{6.91}{k}$ )

Also half-life for a first-order is given by

$t_{1 / 2}=\frac{0.693}{k} \Rightarrow k=\frac{0.693}{1}=0.693$

$\Rightarrow t=\frac{6.91}{0.693} \approx 10 \mathrm{~min}$$

Hence, the correct answer is option 1) 10 minutes.

Question 2: If the rate constant of a reaction is $0.03 \mathrm{~s}^{-1}$. how much time does it take for $7.2 \mathrm{~mol} \mathrm{~L}^{-1}$ concentration of the reactant to get reduced to $0.9 \mathrm{~mol} \mathrm{L}^{-1}$ ? (Given: $\log 2=0.3$) (NEET 2025)

Options

1. 21.0 s

2. 69.3 s

3. 23.1 s

4. 210 s

Answer: Given that

Initial concentration $[R]_0 = 7.2 \ \mathrm{mol \, L^{-1}}$
Final concentration $[R] = 0.9 \ \mathrm{mol \, L^{-1}}$
Rate constant $k = 0.03 \ \mathrm{s^{-1}}$
Given $\log 2 = 0.3$

Since the units of $k$ are $\mathrm{s^{-1}}$, this is a first-order reaction.

Formula: $t = \frac{2.303}{k} \log \left( \frac{[R]_0}{[R]} \right)$

Substitute: $t = \frac{2.303}{0.03} \log \left( \frac{7.2}{0.9} \right)$

This becomes $t = \frac{2.303}{0.03} \log(8)$

Now, $\log(8) = \log(2^3) = 3 \log 2 = 3 \times 0.3 = 0.9$

So, $t = \frac{2.303}{0.03} \times 0.9 = 76.77 \times 0.9 = \mathbf{69.093 \ \mathrm{s}}$

Hence, the correct answer is option 2) 69.3 s.

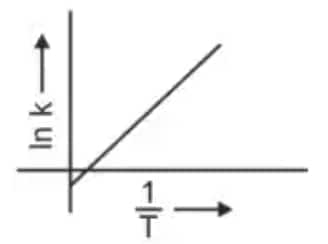
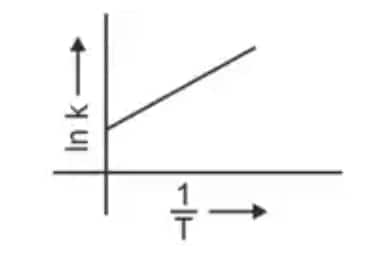
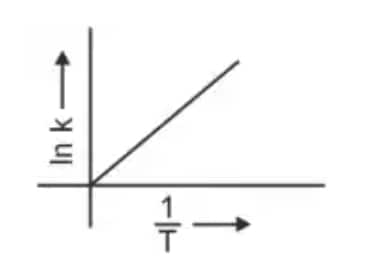
Question 3: Which plot of In k vs 1/T is consistent with the Arrhenius equation? (NEET 2024)

Options

3.

4.

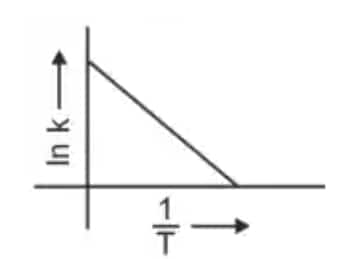
Answer: The Arrhenius equation is given as

$k = A e^{-\frac{E_a}{RT}}$

In $k$ vs $\frac{1}{T}$ gives a straight-line graph with slope $= -\frac{E_a}{R}$ and intercept $= \ln A$.

Hence, the correct answer is option (4)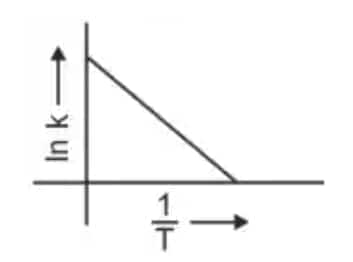

Question 4: For a certain reaction, the rate $R = k[A]^2[B]$, when the initial concentration of A is tripled, keeping the concentration of B constant, the initial rate would be: (NEET 2023)

Options

1. decrease by a factor of nine.

2. increase by a factor of six.

3. increase by a factor of nine

4. increase by a factor of three

Answer: $R = k[A]^2[B]$

$r \propto [A]^2$, if $[B]$ remains constant

$r_f \propto [3A]^2$

$r_f \propto 9 \times [A]^2 \propto 9 \times r_i$

So, the rate will increase 9 times the initial rate.

Hence, the correct answer is option (3), increase by a factor of nine.

Question 5: Given below are two statements: one is labeled as Assertion A and the other is labeled as Reason R :
Assertion A: A reaction can have zero activation energy.
Reasons R: The minimum extra amount of energy absorbed by reactant molecules so that their energy becomes equal to the threshold value is called activation energy.

In light of the above statements, choose the correct answer from the options given below: (NEET 2023)

Options

1. Both A and R are true, and R is the correct explanation of A.

2. Both A and R are true, and R is NOT the correct explanation of A.

3. A is true, but R is false.

4. A is false, but R is true.

Answer: The free radical reactions can have zero activation energy. In the free radical combination reaction in termination, steps have $E_a = 0$.

Hence, the correct answer is option (2), Both A and R are true, and R is NOT the correct explanation of A.

Question 6: For a first-order reaction $\mathrm{A} \rightarrow$ Products, the initial concentration of A is 0.1 M, which becomes 0.001 M after 5 minutes. Rate constant for the reaction in $\mathrm{min}^{-1}$ is: (NEET 2022)

Options

1. 0.9212

2. 0.4606

3. 0.2303

4. 1.3828

Answer: For a first-order reaction, the integrated rate law expression is

$\begin{aligned} & \ln \left(\frac{\mathrm{A}_0}{\mathrm{~A}_{\mathrm{t}}}\right)=\mathrm{Kt} \\ & \Rightarrow \quad \ln \left(\frac{0.1}{0.001}\right)=\mathrm{K}(5) \\ & \Rightarrow \mathrm{K}=\frac{\ln 100}{5}=\frac{4.606}{5}=0.9212 \mathrm{~min}^{-1}\end{aligned}$

Hence, the correct answer is option (1), 0.9212.

Question 7: The given graph is a representation of the kinetics of a reaction

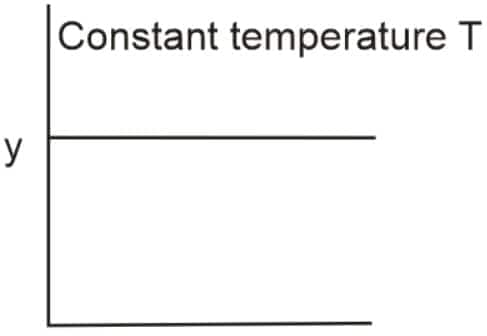
The y and x axes for zero and first-order reactions, respectively, are: (NEET 2022)

Options

1. zero order (y= concentration and x= time), first order (y= rate constant and x= concentration)

2. zero order ( $\mathrm{y}=$ rate and $\mathrm{x}=$ concentration $)$, first order $\left(\mathrm{y}=t_{1 / 2}\right.$ and $\mathrm{x}=$ concenration $)$

3. zero order ( $y=$ rate and $x=$ concentration), first order ( $y=$ rate and $x=t_{1 / 2}$ )

4. zero order ( $y=$ concentration and $x=$ time $)$, first order $\left(y=t_{1 / 2}\right.$, and $x=$ concentration $)$

Answer: For a zero-order reaction:
Rate $\propto [\mathrm{A}]^0$
$\Rightarrow \text{Rate} = k = \text{constant}$
$\Rightarrow$ Rate is independent of concentration.

For a first-order reaction:
$t_{1/2} = \frac{\ln 2}{k}$
$\Rightarrow$ Half-life is independent of concentration.

Hence, the correct answer is option (2), zero order ( $\mathrm{y}=$ rate and $\mathrm{x}=$ concentration $)$, first order $\left(\mathrm{y}=t_{1 / 2}\right.$ and $\mathrm{x}=$ concenration $)$.

Question 8: The slope of the Arrhenius Plot $\ln k \, v/s \; \frac{1}{T}$ the first-order reaction is $-5 \times 10^{3} \, K$. The value of $E_a$ of the reaction is. Choose the correct option for your answer. (NEET 2021)

[Given $R = 8.314 \ \mathrm{J \, K^{-1} \, mol^{-1}}$]

Options:

1. \( 41.5 \ \text{kJ mol}^{-1} \)

2. \( 83.0 \ \text{kJ mol}^{-1} \)

3. \( 166 \ \text{kJ mol}^{-1} \)

4. \( -83 \ \text{kJ mol}^{-1} \)

Answer: According to the Arrhenius equation

\( k = Ae^{-E_a/RT} \)

\( \ln k = \ln A + \ln e^{-E_a/RT} \)

\( \ln k = \ln A - \frac{E_a}{R} \left( \frac{1}{T} \right) \)

The slope \( \left( \ln k \ \text{vs} \ \frac{1}{T} \right) \) of the above equation

\( m = -\frac{E_a}{R} \)

Given, \( m = -5 \times 10^3 \ \text{K} \) and \( R = 8.314 \ \text{J K}^{-1} \text{mol}^{-1} \)

\( -5 \times 10^3 = -\frac{E_a}{8.314} \)

\( E_a = 5 \times 10^3 \times 8.314 \ \text{J/mol} \)

\( E_a = 41.57 \times 10^3 \ \text{J/mol} \)

\( E_a = 41.5 \ \mathrm{kJ \ mol^{-1}} \)

Hence, the correct answer is option (1), \( 41.5 \ \text{kJ mol}^{-1} \).

Question 9: An increase in the concentration of the reactants of a reaction leads to a change in: (NEET 2020)

Options

1. Collision frequency

2. Activation energy

3. heat of reaction

4. threshold energy

Answer: An increase in the concentration of the reactants leads to an increase in the collision frequency. Threshold energy, activation energy, and heat of reaction are not affected by the increase in concentration. This is because, due to the increase in concentration, the number of particles increases and hence the number of collisions.

Hence, the correct answer is option (1), Collision frequency.

Question 10: The rate constant for a first-order reaction is $4.606 \times 10^{-3} \mathrm{~s}^{-1}$. The time required to reduce $2 g$ of the reactant to $0.2 g$ is: (NEET 2020)

Options

1. 1000s

2. 100s

3. 200s

4. 500s

Answer: We are given:

$K = 4.606 \times 10^{-3} \ \mathrm{s}^{-1}$

Thus, the reaction is of the first order.

We have:

$K t = \ln \frac{A_0}{A_t}$

$4.606 \times 10^{-3} \ t = 2.303 \ \log \left( \frac{2}{0.2} \right)$

Thus, $t = 0.5 \times 10^3 \ \mathrm{s}$

$t = 500 \ \mathrm{s}$

Hence, the correct answer is option (4), 500s.

Important Topics of Chemical Kinetics

Chemical Kinetics is a scoring unit in chemistry. It is among the do-or-die chapters for NEET. Questions in the NEET 2024 question paper come from the Chemical Kinetics unit. Chemical kinetics NEET PYQ includes questions on how reactions occur and the different factors affecting them. Students thinking about how to study chemistry for NEET should start with this unit. Given below are a few important topics from this unit.

Tips while Solving Chemical Kinetics NEET PYQ

Solving previous year questions regularly builds confidence. It helps students understand the types of questions asked in the exam. Aspirants can start by solving the 20 important NEET chemistry questions to make their preparation strong. Given below are a few tips that they can use to solve NEET chemical kinetics previous year questions.

1. Students have to understand how to obtain rate laws from the rate-determining step. Accessing the NEET chemistry mock test improves score and speed.

2. Learn how to determine the order of a reaction from experimental data and not just by stoichiometry.

3. Get familiar with the rate equations for zero, first, and second-order reactions. Study only from the Chemistry books for NEET to avoid confusion.

4. Understand the role of activation energy and how it plays a part in the rate determination. Try to apply the Arrhenius equation to the temperature changes.

5. Solve NEET PYQ chemical kinetics by using the NEET chemistry question paper.

6. Prepare flashcards of important formulas for NEET chemistry. This helps to answer NEET chemical kinetics previous year questions confidently.